Polarization and polarization analysis

Jacques Schweizer

CEA-Grenoble, DSM/DRFMC/SPSMS/MDN, 38054 Grenoble Cedex 9, France

The neutron carries a spin , which is an internal angular momentum with the quantum number s=1/2 This means that the eigenvalues of operator ² is s(s+1)²=3/4² and the eigen values of operator sz are ms = ±1/2 .

Pauli matrices are the matrices representing the operator

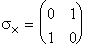
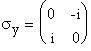
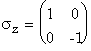
The neutron carries a magnetic moment where is the nuclear Bohr magneton and = -1.913 is the value of the neutron magnetic moment expressed in nuclear Bohr magnetons.

The gyromagnetic ratio of the neutron , which has not to be confused with , is the ratio between the magnetic moment and the spin moment:

= -1.832 10⁸ rad s^-1 T^-1

and are both negative, which means that the magnetic moments and the spin of the neutron are opposed one to the other.

If |+> and |-> represent the 2 states "up" and "down" along Oz, corresponding to ms =1/2 and
ms =-1/2, the spin wave function of a neutron can be written:

|c> = a|+> + b|->

(7)

where a and b are two complex quantities such |a|² + |b|² =1.

The polarization of one neutron is defined as = <> = <>, where < > means the quantum average value. This vectorial relation stands for:

p_x = <s_x>

p_y = <s_y>

p_z = <s_z>

It is very important to note that, contrarily to and which are quantum operators, the polarization , the components of which are quantum average values, is a classical vector, and can be treated consequently.

It is therefore possible to prepare a neutron beam in such a way that it is polarized along a given direction. It is also possible to analyze the direction of a scattered beam.

We shall review the different methods using polarization :

-polarized neutrons without polarization analysis

-longitudinal polarization analysis when the polarization of the scattered beam is analyzed along the direction of the incoming polarization

-spherical (or 3-dimension) analysis when the polarization of the scattered beam is analyzed along the 3 directions of space